
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Ostatnio zmodyfikowany 2025-06-01 05:05.
Jeśli parabola ma poziomy osi, standardowa postać równania parabola jest to: (y -k)2 = 4p(x - h), gdzie p≠ 0. The wierzchołek tego parabola jest w (h, k). Koncentruje się na (h + p, k). Kierownica to linia x = h - p.
A więc, jak znaleźć wierzchołek i kierownicę paraboli?
Standardowy formularz to (x - h)2 = 4p (y - k), gdzie Centrum jest (h, k + p) i kierownica jest y= k - p. Jeśli parabola jest obrócony tak, że jego wierzchołek is (h, k) a jego oś symetrii jest równoległa do osi x, ma an równanie z (y - k)2 = 4p (x -h), gdzie Centrum jest (h + p, k) i kierownica jest x = h - p.
Dodatkowo, jakie jest równanie paraboli bocznej? „Ogólna” forma równanie paraboli to ten, do którego jesteś przyzwyczajony, y = ax2 + bx + c - chyba że kwadratowa to bokiem ”, w takim przypadku równanie będzie wyglądać mniej więcej tak: x = ay2 + przez +c.
A więc, jak znaleźć wierzchołek równania paraboli?
Ten punkt, w którym parabola zmienia kierunek, nazywa się „ wierzchołek . Jeśli kwadrat jest zapisany w postaci y = a(x - h)2 + k, następnie wierzchołek jest punktem (h, k). To ma sens, jeśli się nad tym zastanowisz. Część kwadratowa jest zawsze dodatnia (dla prawej strony do góry parabola ), chyba że wynosi zero.
Dla jakiej wartości p ma wierzchołek paraboli?
Absolut wartość p jest odległość między wierzchołek a ostrość i odległość między wierzchołek i kierownica. (znak na P mówi mi, w jaki sposób parabola twarze.) Ponieważ ognisko i kierownica są od siebie oddalone o dwie jednostki, odległość ta musi wynosić jedną jednostkę, więc | P | = 1.
Zalecana:
Jak przekonwertować standardowy wierzchołek na formę podzieloną na czynniki?

Konwersja między różnymi formami kwadratu - Expii. Standardowa forma to ax^2 + bx + c. Forma wierzchołka to a(x-h)^2 + k, która ujawnia wierzchołek i oś symetrii. Forma rozkładana na czynniki to a(x-r)(x-s), która ujawnia pierwiastki
Jak znaleźć wierzchołek i Directrix?

Standardowa forma to (x - h)2 = 4p (y - k), gdzie ognisko to (h, k + p), a kierownica to y = k - p. Jeśli parabola jest obrócona tak, że jej wierzchołek jest (h,k), a jej oś symetrii jest równoległa do osi x, to ma równanie (y - k)2 = 4p (x - h), gdzie ognisko to (h + p, k), a kierownica to x = h - p
Jak oznaczysz wierzchołek i oś symetrii?
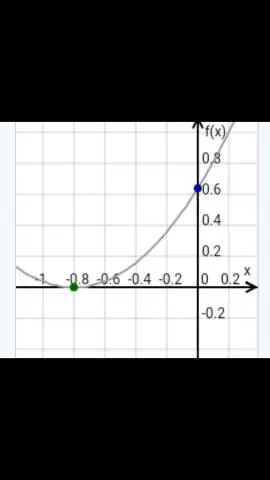
Oś symetrii zawsze przechodzi przez wierzchołek paraboli. Współrzędna x wierzchołka jest równaniem osi symetrii paraboli. Dla funkcji kwadratowej w postaci standardowej, y=ax2+bx+c, oś symetrii jest linią pionową x=−b2a
Jak narysować stożek paraboli?
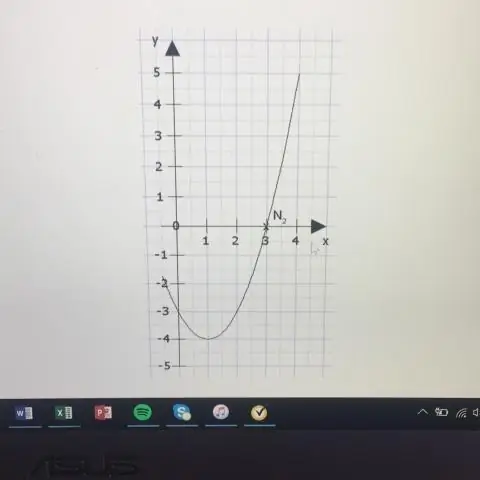
Kierownicą jest linia y = k - p. Oś to linia x = h. Jeśli p > 0, parabola otwiera się w górę, a jeśli p < 0, parabola otwiera się w dół. Jeśli parabola ma oś poziomą, standardową postacią równania paraboli jest: (y - k)2 = 4p(x - h), gdzie p≠ 0
Jak zrobić przekrój stożkowy paraboli?
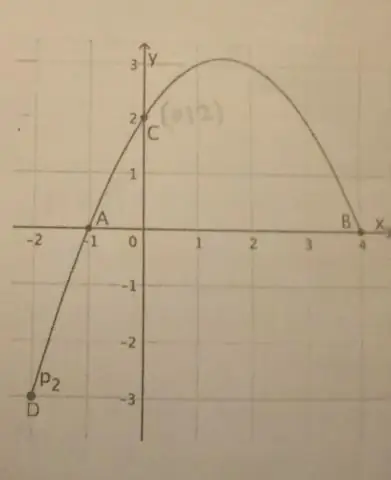
Jeśli parabola ma oś pionową, standardową postacią równania paraboli jest: (x - h)2 = 4p(y - k), gdzie p≠ 0. Wierzchołek tej paraboli to (h, k). Fokus znajduje się w (h, k + p). Kierownicą jest linia y = k - p
