Wideo: Jak zrobić przekrój stożkowy paraboli?
2024 Autor: Miles Stephen | [email protected]. Ostatnio zmodyfikowany: 2023-12-15 23:39
Jeśli parabola ma oś pionową, standardową postać równania parabola jest to: (x - h)2 = 4p(y - k), gdzie p≠ 0. Wierzchołek tego parabola jest w (h, k). Fokus znajduje się w (h, k + p). Kierownicą jest linia y = k - p.
Ludzie pytają też, czy parabola to przekrój stożkowy?
ten parabola jest kolejnym powszechnie znanym sekcja stożkowa . Geometryczna definicja a parabola jest miejscem wszystkich punktów, tak aby znajdowały się w równej odległości od punktu, zwanego ogniskiem, i prostej, zwanej kierownicą. Innymi słowy ekscentryczność parabola jest równy 1.
Dodatkowo jakie są 4 rodzaje przekrojów stożkowych? Cztery sekcje stożkowe są kręgi , elipsy, parabole i hiperbole. Przekroje stożkowe były badane od dłuższego czasu. Kepler po raz pierwszy zauważył, że planety mają orbity eliptyczne. W zależności od energii ciała orbitującego możliwe są kształty orbit, które są jednym z czterech typów przekrojów stożkowych.
Podobnie, jak zrobić sekcję stożkową?
Sekcje stożkowe są generowane przez przecięcie płaszczyzny ze stożkiem. Jeżeli płaszczyzna jest równoległa do osi obrotu (oś y), to sekcja stożkowa jest hiperbolą. Jeżeli płaszczyzna jest równoległa do linii generującej, sekcja stożkowa jest parabolą.
Jaka jest standardowa forma paraboli?
f(x) = a(x-h)2 + k, gdzie (h, k) jest wierzchołkiem parabola . FYI: Różne podręczniki mają różne interpretacje odniesienia” forma standardowa " funkcji kwadratowej. Niektórzy mówią, że f (x) = ax2 + bx + c to " forma standardowa ”, podczas gdy inni mówią, że f (x) = a(x - h)2 + k to " forma standardowa ".
Zalecana:
Jaki jest przekrój sześcianu?
Pojedynczy punkt (wierzchołek sześcianu) odcinek (krawędź sześcianu) trójkąt (jeżeli przecinają się trzy sąsiednie ściany sześcianu) równoległobok (jeżeli przecinają się dwie pary przeciwległych ścian – obejmuje to romb lub prostokąt) trapez (jeśli dwie pary
Jak znaleźć przekrój kwadratu?
WIDEO Mając to na uwadze, jaki jest przekrój kwadratu? Przekroje . A Przekrój to kształt, który uzyskujemy, gdy przecinamy obiekt na wprost. ten Przekrój tego obiektu jest trójkątem. Jest to jak zajrzenie do wnętrza czegoś przez przecięcie.
Czym jest cienki przekrój w geologii?
W mineralogii optycznej i petrografii cienki przekrój (lub cienki przekrój petrograficzny) to laboratoryjne przygotowanie próbki skały, minerału, gleby, ceramiki, kości, a nawet metalu do użycia z polaryzacyjnym mikroskopem petrograficznym, mikroskopem elektronowym i mikrosondą elektronową
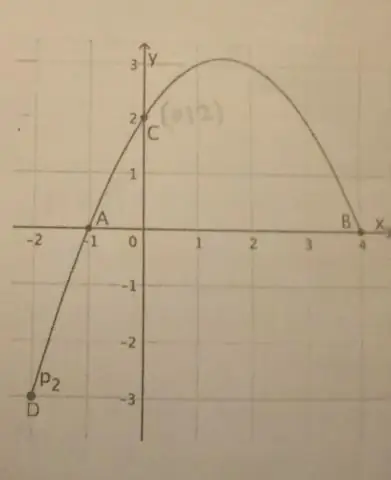
Jak narysować stożek paraboli?
Kierownicą jest linia y = k - p. Oś to linia x = h. Jeśli p > 0, parabola otwiera się w górę, a jeśli p < 0, parabola otwiera się w dół. Jeśli parabola ma oś poziomą, standardową postacią równania paraboli jest: (y - k)2 = 4p(x - h), gdzie p≠ 0
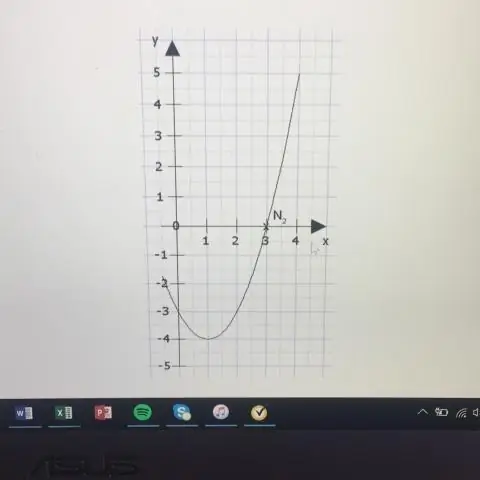
Jak znaleźć wierzchołek paraboli poziomej?
Jeśli parabola ma oś poziomą, standardową postacią równania paraboli jest: (y -k)2 = 4p(x - h), gdzie p≠ 0. Wierzchołek tej paraboli to (h, k). Koncentruje się na (h + p, k). Kierownica to linia x = h - p