
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Ostatnio zmodyfikowany 2025-01-22 17:07.
Kierownica . A parabola to zbiór wszystkich punktów na płaszczyźnie, które są w równej odległości od danego punktu i danej prostej. Punkt nazywa się ogniskiem parabola , a linia nazywa się kierownica . ten kierownica jest prostopadła do osi symetrii a parabola i nie dotyka parabola.
Co więcej, jak znaleźć Directrix paraboli?
Standardowy formularz to (x - h)2 = 4p (y - k), gdzie ognisko jest (h, k + p) i kierownica jest y = k - p. Jeśli parabola jest obrócony tak, że jego wierzchołek jest (h, k), a jego oś symetrii jest równoległa do osi x, ma równanie (y - k)2 = 4p (x - h), gdzie ognisko jest (h + p, k) i the kierownica jest x = h - p.
Jak znaleźć formę wierzchołkową paraboli? f(x) = a(x-h)2 + k, gdzie (h, k) to wierzchołek z parabola . FYI: Różne podręczniki mają różne interpretacje odniesienia „standard Formularz " funkcji kwadratowej. Niektórzy mówią, że f (x) = ax2 + bx + c to „standardowy Formularz ”, podczas gdy inni mówią, że f (x) = a(x - h)2 + k to „standardowy Formularz ".
Podobnie można zapytać, czym jest Directrix hiperboli?
W przypadku hiperbola , a kierownica jest linią prostą, w której odległość od każdego punktu na hiperbola do jednego z jego dwóch ognisk jest krotnością prostopadłej odległości od do kierownica , gdzie jest stałą większą niż. Zauważ, że hiperbole mają dwa ogniska i dwie kierownice, po jednym dla każdego ogniska.
Jak znaleźć Directrix równania?
Standardowy formularz to (x - h)2 = 4p (y - k), gdzie ognisko jest (h, k + p) i the kierownica jest y = k - p. Jeśli parabola jest obrócona tak, że jej wierzchołek jest (h, k), a jej oś symetrii jest równoległa do osi x, ma równanie z (y - k)2 = 4p (x - h), gdzie ognisko jest (h + p, k) i kierownica jest x = h - p.
Zalecana:
Jak znaleźć wierzchołek i Directrix?

Standardowa forma to (x - h)2 = 4p (y - k), gdzie ognisko to (h, k + p), a kierownica to y = k - p. Jeśli parabola jest obrócona tak, że jej wierzchołek jest (h,k), a jej oś symetrii jest równoległa do osi x, to ma równanie (y - k)2 = 4p (x - h), gdzie ognisko to (h + p, k), a kierownica to x = h - p
Jaki jest maksymalny lub minimalny punkt paraboli?

Parabole pionowe dostarczają ważnej informacji: kiedy parabola się otwiera, wierzchołek jest najniższym punktem na wykresie - nazywanym minimum lub min. Kiedy parabola otwiera się w dół, wierzchołek jest najwyższym punktem na wykresie - nazywanym maksimum lub maksimum
Jak narysować stożek paraboli?
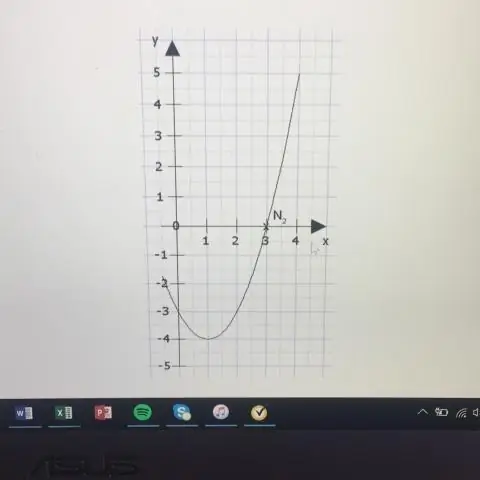
Kierownicą jest linia y = k - p. Oś to linia x = h. Jeśli p > 0, parabola otwiera się w górę, a jeśli p < 0, parabola otwiera się w dół. Jeśli parabola ma oś poziomą, standardową postacią równania paraboli jest: (y - k)2 = 4p(x - h), gdzie p≠ 0
Jak znaleźć wierzchołek paraboli poziomej?

Jeśli parabola ma oś poziomą, standardową postacią równania paraboli jest: (y -k)2 = 4p(x - h), gdzie p≠ 0. Wierzchołek tej paraboli to (h, k). Koncentruje się na (h + p, k). Kierownica to linia x = h - p
Jak zrobić przekrój stożkowy paraboli?
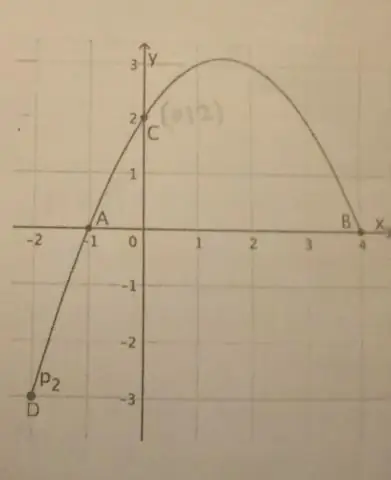
Jeśli parabola ma oś pionową, standardową postacią równania paraboli jest: (x - h)2 = 4p(y - k), gdzie p≠ 0. Wierzchołek tej paraboli to (h, k). Fokus znajduje się w (h, k + p). Kierownicą jest linia y = k - p
