
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Ostatnio zmodyfikowany 2025-01-22 17:07.
Aby określić identyczność różnicy dla stycznej, użyj faktu, że tan(−β) = −tanβ
- Przykład 1: Znajdź dokładną wartość dębnik 75°.
- Przykład 2: Sprawdź, czy dębnik (180° − x) = − dębnik x.
- Przykład 3: Sprawdź, czy dębnik (180° + x) = dębnik x.
- Przykład 4: Sprawdź, czy dębnik (360° − x) = − dębnik x.
- Przykład 5: Sprawdź tożsamość .
Poza tym, jaki jest wzór na styczną?
W dowolnym trójkącie prostokątnym tangens kąta to długość przeciwległego boku (O) podzielona przez długość sąsiedniego boku (A). W formuła , jest napisane po prostu jako „tan”. Często zapamiętywany jako "SOH" - co oznacza, że sinus jest przeciwieństwem hipotensyjności.
Dodatkowo, jak przepisać styczną? Aby przepisać funkcję sinus pod względem stycznej, wykonaj następujące kroki:
- Zacznij od tożsamości współczynnika obejmującej sinus, cosinus i tangens, a następnie pomnóż każdy bok przez cosinus, aby otrzymać sinus po lewej stronie.
- Zastąp cosinus jego funkcją odwrotną.
- Rozwiąż pitagorejską tożsamość tan2θ + 1 = s2θ dla siecznej.
Jaka jest w związku z tym formuła podwójnego kąta?
O transkrypcji. Cosinus formuła podwójnego kąta mówi nam, że cos(2θ) jest zawsze równe cos²θ-sin²θ. Na przykład cos(60) jest równe cos²(30)-sin²(30). Możemy użyć tej tożsamości do przepisywania wyrażeń lub rozwiązywania problemów.
Jaka jest tożsamość styczna?
Suma tożsamość dla tangens wyprowadza się w następujący sposób: Aby określić różnicę tożsamość dla tangens , wykorzystaj fakt, że dębnik (−β) = −tanβ. Podwójny kąt tożsamość dla tangens uzyskuje się za pomocą sumy tożsamość dla tangens . Półkąt tożsamość dla tangens można napisać w trzech różnych formach.
Zalecana:
Jaka jest jedna rzecz, która decyduje o tożsamości atomu?

Pamiętaj, że liczba protonów w jądrze decyduje o tożsamości elementu. Zmiany chemiczne nie wpływają na jądro, więc zmiany chemiczne nie mogą zmienić jednego typu atomu w inny. Zmienia się zatem tożsamość atomu. Przypomnijmy, że jądro atomu zawiera protony i neutrony
Jak rozwiązujesz własność tożsamości?

Własność tożsamości składa się z dwóch części: tożsamości addytywnej i tożsamości multiplikatywnej. Dodaj zero (0) do liczby, suma to ta liczba. Pomnóż liczbę przez 1, Produkt jest tą liczbą. Podziel liczbę przez samą, iloraz wynosi 1
Czym są tożsamości wielomianowe?

Tożsamości wielomianowe to równania, które są prawdziwe dla wszystkich możliwych wartości zmiennej. Na przykład x²+2x+1=(x+1)² jest tożsamością. Ten film wprowadzający zawiera więcej przykładów tożsamości i omawia, w jaki sposób dowodzimy, że równanie jest tożsamością
Jak zamienić macierz w macierz tożsamości?

WIDEO Co więcej, jak znaleźć odwrotność macierzy za pomocą macierzy tożsamości? Działa to w ten sam sposób dla matryce . Jeśli pomnożysz a matryca (takich jak A) i jego odwrotność (w tym przypadku A – 1 ), otrzymujesz macierz jednostkowa I.
Jaki jest przykład własności tożsamości mnożenia?
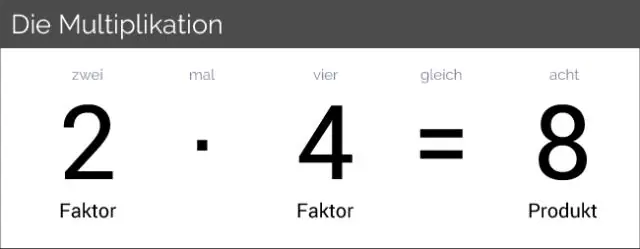
Własność tożsamości mnożenia: Iloczynem 1 i dowolnej liczby jest ta liczba. Na przykład 7 × 1 = 7 7 imes 1 = 7 7×1=77, times, 1, equals, 7
