
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Ostatnio zmodyfikowany 2025-01-22 17:07.
Tożsamości wielomianowe są równaniami, które są prawdziwe dla wszystkich możliwych wartości zmiennej. Na przykład x²+2x+1=(x+1)² to an tożsamość . Ten film wprowadzający zawiera więcej przykładów tożsamości i omawia, w jaki sposób dowodzimy, że równanie jest tożsamość.
Czym więc są ważne tożsamości?
Jeśli równanie zawiera jedną lub więcej zmiennych i jest ważny dla wszystkich wartości zastępczych zmiennych, dla których zdefiniowane są obie strony równania, to równanie jest znane jako an tożsamość . Równanie x 2 + 2 x = x(x + 2), na przykład to an tożsamość ponieważ to jest ważny dla wszystkich wartości zastępczych x.
Następnie pojawia się pytanie, co to jest wzór wielomianowy? Wzór na równania wielomianowe Zwykle równanie wielomianowe jest wyrażony w postaci a (x). Przykład równanie wielomianowe to: 2x2 + 3x + 1 = 0, gdzie 2x2 + 3x + 1 to w zasadzie a wielomian wyrażenie, które zostało ustawione na zero, tworząc a równanie wielomianowe.
Co więcej, jakie są tożsamości algebraiczne?
jakiś tożsamość algebraiczna jest równością, która obowiązuje dla dowolnych wartości jego zmiennych. Na przykład tożsamość (x + y) 2 = x 2 + 2 xy + y 2 (x+y)^2 = x^2 + 2xy + y^2 (x+y)2=x2+2xy+y2 obowiązuje dla wszystkich wartości x i y.
Jak zweryfikować tożsamość algebraiczną?
Tożsamość algebraiczna (a+b)2 = a2 + 2ab + b2 jest zweryfikowany. ten tożsamość (a+b)2 = a2 + 2ab + b2 jest weryfikowana poprzez wycinanie i wklejanie papieru. Ten tożsamość można zweryfikować geometrycznie, przyjmując inne wartości a i b.
Zalecana:
Jaka jest jedna rzecz, która decyduje o tożsamości atomu?

Pamiętaj, że liczba protonów w jądrze decyduje o tożsamości elementu. Zmiany chemiczne nie wpływają na jądro, więc zmiany chemiczne nie mogą zmienić jednego typu atomu w inny. Zmienia się zatem tożsamość atomu. Przypomnijmy, że jądro atomu zawiera protony i neutrony
Jak rozwiązujesz własność tożsamości?

Własność tożsamości składa się z dwóch części: tożsamości addytywnej i tożsamości multiplikatywnej. Dodaj zero (0) do liczby, suma to ta liczba. Pomnóż liczbę przez 1, Produkt jest tą liczbą. Podziel liczbę przez samą, iloraz wynosi 1
Jak zamienić macierz w macierz tożsamości?

WIDEO Co więcej, jak znaleźć odwrotność macierzy za pomocą macierzy tożsamości? Działa to w ten sam sposób dla matryce . Jeśli pomnożysz a matryca (takich jak A) i jego odwrotność (w tym przypadku A – 1 ), otrzymujesz macierz jednostkowa I.
Jak rozwiązujesz tożsamości Tan?

Aby określić identyczność różnicy dla stycznej, użyj faktu, że tan(−β) = −tanβ. Przykład 1: Znajdź dokładną wartość tan 75°. Przykład 2: Sprawdź, czy tan (180° − x) = −tan x. Przykład 3: Sprawdź, czy tan (180° + x) = tan x. Przykład 4: Sprawdź, czy tan (360° − x) = − tan x. Przykład 5: Zweryfikuj tożsamość
Jaki jest przykład własności tożsamości mnożenia?
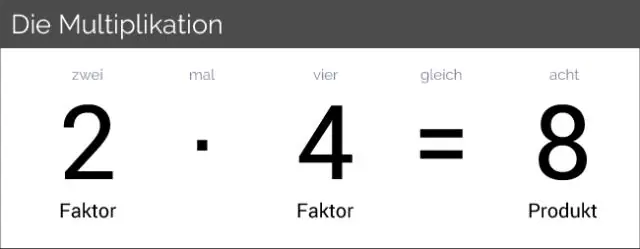
Własność tożsamości mnożenia: Iloczynem 1 i dowolnej liczby jest ta liczba. Na przykład 7 × 1 = 7 7 imes 1 = 7 7×1=77, times, 1, equals, 7
