
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Ostatnio zmodyfikowany 2025-01-22 17:07.
Porównując dwie populacje, im większe odchylenie standardowe, tym większa dyspersja rozkład ma, pod warunkiem, że zmienna będąca przedmiotem zainteresowania niż dwie populacje ma ten sam zestaw miar.
Tak więc, co to jest odchylenie standardowe używane w połączeniu?
ten odchylenie standardowe jest używany w połączeniu z MEAN do numerycznego opisu rozkładów, które mają kształt dzwonka. ŚREDNIA mierzy środek? dystrybucja, podczas gdy odchylenie standardowe mierzy ROZPRZESIĘCIE dystrybucji.
Co więcej, jaka jest empiryczna reguła w statystyce? ten Zasada empiryczna stwierdza, że w przypadku rozkładu normalnego prawie wszystkie dane mieszczą się w zakresie trzech odchyleń standardowych średniej. ten Zasada empiryczna można podzielić na trzy części: 68% danych mieści się w pierwszym odchyleniu standardowym od średniej. 95% mieści się w dwóch odchyleniach standardowych.
W związku z tym, jakie jest ograniczenie zakresu jako miary rozproszenia?
ZASIĘG . ten zasięg to różnica między największą i najmniejszą obserwacją w danych. Główna zaleta tego miara dyspersji jest to, że łatwo to obliczyć. Z drugiej strony ma wiele wad.
Co reprezentuje liczbę odchyleń standardowych obserwacji od średniej?
Z-score jest często nazywany wartością standaryzowaną. Z-score mierzy liczba obserwacji odchyleń standardowych jest powyżej lub poniżej mieć na myśli . Były. Z-score1,24 jest interpretowany jako „wartość danych wynosi 1,24 odchylenie standardowe wyżej mieć na myśli ."
Zalecana:
Jak obliczyć odchylenie standardowe od PMP?

Formuła stosowana w PMBOK na odchylenie standardowe jest prosta. To tylko (P-O)/6. Jest to pesymistyczna ocena aktywności minus optymistyczna ocena aktywności podzielona przez sześć. Problem polega na tym, że ten kształt w żaden sposób nie tworzy miary odchylenia standardowego
Jakie jest odchylenie standardowe używane w połączeniu z?
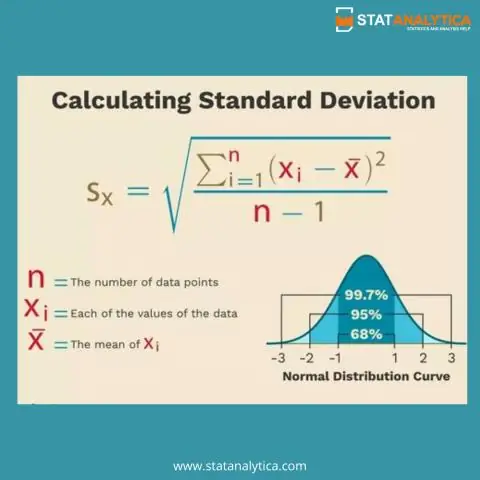
Odchylenie standardowe jest używane w połączeniu ze ŚREDNĄ do numerycznego opisania rozkładów w kształcie dzwonu. ŚREDNIA mierzy środek? rozkład, podczas gdy odchylenie standardowe mierzy SPREAD rozkładu
Jak obliczyć odchylenie standardowe w SPC?

Obliczanie odchylenia standardowego Oblicz średnią procesu μ Odejmij średnią procesu od każdej zmierzonej wartości danych (wartości X i) Podnieś do kwadratu każde z odchyleń obliczonych w kroku 2. Dodaj wszystkie kwadraty odchyleń obliczone w kroku 3. Podziel wynik krok 4 według wielkości próbki
Czy odchylenie standardowe S kwadrat?

Odchylenie standardowe (S) = pierwiastek kwadratowy z wariancji Odchylenie standardowe jest miarą rozrzutu najczęściej stosowaną w praktyce statystycznej, gdy średnia jest używana do obliczania tendencji centralnej. W ten sposób mierzy rozłożone wokół średniej
Jak znaleźć odchylenie standardowe i średnią w programie Excel?
Odchylenie standardowe jest miarą tego, jaka jest wariancja w zbiorze liczb w porównaniu ze średnią (średnią) liczb. Aby obliczyć odchylenie standardowe w programie Excel, możesz użyć jednej z dwóchfunkcje podstawowe, w zależności od zestawu danych. Jeśli dane reprezentują całą populację, możesz użyć STDEV. Funkcja P
