Wideo: Jaki jest przykład liczby wymiernej, która nie jest liczbą całkowitą?
2024 Autor: Miles Stephen | [email protected]. Ostatnio zmodyfikowany: 2023-12-15 23:39
A racjonalny ” numer to stosunek dwóch liczb całkowitych. Do przykład , następujące są liczby wymierne , a żadna z nich nie jest liczbą całkowitą: 1 / 2. 2 / 3.
Pytanie brzmi również, co to jest liczba wymierna, która nie jest liczbą całkowitą?
Wszystkie ujemne liczby całkowite to liczby wymierne ale to są nie liczby całkowite . Na przykład -3 to a Liczba wymierna (można wyrazić jako -3/1), ale jest nie liczba całkowita . Ułamki takie jak 1/2, -3/4, 22/7 itd.
Po drugie, czy minus 3 jest liczbą wymierną? − 3 jest ujemne więc to nie jest naturalna ani całość numer . Liczby wymierne są liczby który może być wyrażony jako ułamek lub stosunek dwóch liczb całkowitych. Liczby wymierne są oznaczone jako Q. Ponieważ − 3 można zapisać jako − 3 1 można argumentować, że − 3 jest również prawdziwy numer.
Po drugie, czym jest liczba wymierna, która jest liczbą całkowitą?
Każdy cały numer jest Liczba wymierna : na przykład 3=31. Więc tak jest racjonalny . Każdy cały numer n można zapisać jako ułamek liczb całkowitych: n=n1. Nie musimy pisać tego w ten sposób; musimy tylko wiedzieć, że da się wyrazić wszystko cały numer jako ułamek liczb całkowitych, a więc jest racjonalny.
Czy liczba wymierna może być liczbą całkowitą, ale nie liczbą całkowitą?
Zestaw wszystkie liczby = {0, 1, 2, 3, 4, …} Wszystkie liczby są tylko liczby całkowite które nie są negatywne. Używając notacji zbiorowej, my Móc powiedz, że zestaw liczby całkowite jest podczas gdy zbiór wszystkie liczby jest w zasadzie. Wracając więc do pytania; Nie , jest brak liczby wymiernej, która nie jest liczbą całkowitą, ale jest cały numer.
Zalecana:
Co to jest liczba naturalna i liczba całkowita na przykładzie?
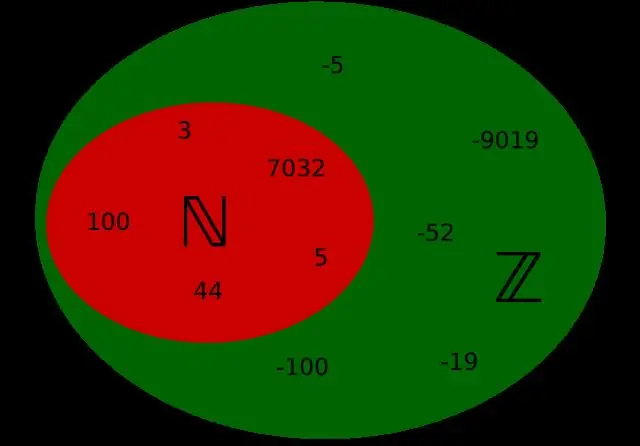
Liczby naturalne to wszystkie liczby 1, 2, 3, 4… Są to liczby, które zwykle liczysz i będą ciągnąć się w nieskończoność. Liczby całkowite to wszystkie liczby naturalne zawierające 0, np. 0, 1, 2, 3, 4… Liczby całkowite obejmują wszystkie liczby całkowite i ich ujemny odpowiednik, np.
Jak obliczyć całkowitą pojemność całkowitą?
Potencjał procesu Oblicza się je za pomocą następującego wzoru: Potencjał ludzki = rzeczywiste godziny pracy x wskaźnik obecności x bezpośrednia stawka pracy x ekwiwalent siły roboczej. Wydajność maszyny = godziny pracy x szybkość pracy x liczba maszyn
Czym są liczby naturalne liczby całkowite i liczby wymierne?
Liczby rzeczywiste dzieli się głównie na liczby wymierne i niewymierne. Liczby wymierne obejmują wszystkie liczby całkowite i ułamki. Wszystkie ujemne liczby całkowite i liczby całkowite składają się na zbiór liczb całkowitych. Liczby całkowite składają się ze wszystkich liczb naturalnych i zera
Czy każda liczba naturalna jest liczbą całkowitą?
Tak to prawda. Ponieważ liczby naturalne zaczynają się od 1 i kończą w nieskończoności, gdzie liczby całkowite zaczynają się od 0 i kończą w nieskończoności. 0 jest jedyną liczbą, która jest liczbami całkowitymi, ale nie jest liczbami naturalnymi. Dlatego każda liczba naturalna jest liczbą całkowitą
Jaki jest przykład czystej liczby urojonej?
Czyste liczby urojone Liczba i nie jest bynajmniej sama! Na przykład, 3 i 3i 3i, i 5 isqrt{5} i5 ?i, pierwiastek kwadratowy z, 5,end pierwiastek kwadratowy i −12i są przykładami liczb czysto urojonych lub liczb w postaci bi bi bi, gdzie b jest niezerowa liczba rzeczywista