
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Ostatnio zmodyfikowany 2025-01-22 17:07.
Jak używać eliminacji Gaussa do rozwiązywania układów równań
- Możesz pomnożyć dowolny wiersz za pomocą stała (inna niż zero). mnoży rząd trzy za pomocą -2, aby otrzymać nowy rząd trzeci.
- Możesz zamienić dowolne dwa rzędy. zamienia wiersze pierwszy i drugi.
- Możesz dodać dwa wiersze razem. dodaje wiersze pierwszy i drugi i zapisuje je w wiersz drugi.
Jak zatem działa eliminacja Gaussa?
Swobodnie rozmawiać, Prace eliminacyjne Gaussa od góry do dołu, aby wytworzyć matrycę w formie schodkowej, podczas gdy Gaus -Jordania eliminacja kontynuuje gdzie Gaussa następnie od dołu do góry, aby wytworzyć matrycę w postaci zredukowanej schodkowej. Technika zostanie zilustrowana w poniższym przykładzie.
Co więcej, czym są macierze reguł Cramera? Zasada Cramera dla systemu 2×2 (z dwiema zmiennymi) Zasada Cramera to kolejna metoda, która może rozwiązywać układy równań liniowych za pomocą wyznaczników. Pod względem notacji a matryca to tablica liczb ujęta w nawiasy kwadratowe, podczas gdy wyznacznik to tablica liczb ujęta w dwie pionowe kreski.
Po drugie, jaki jest cel eliminacji Gaussa?
Eliminacja Gaussa . Z Wikipedii, wolnej encyklopedii. Eliminacja Gaussa , znany również jako redukcja wierszy, to algorytm w algebrze liniowej do rozwiązywania układu równań liniowych. Zwykle rozumiany jest jako sekwencja operacji wykonywanych na odpowiedniej macierzy współczynników.
Jaka jest różnica między eliminacją Gaussa i Gaussa Jordana?
3 odpowiedzi. Eliminacja Gaussa pomaga umieścić macierz w postaci schodkowej, podczas gdy Gaus - Eliminacja Jordanii umieszcza macierz w postaci schodkowej o zredukowanej liczbie wierszy. W przypadku małych systemów (lub ręcznych) jest zwykle wygodniejszy w użyciu Gaus - Eliminacja Jordanii i wyraźnie rozwiąż dla każdej reprezentowanej zmiennej w system macierzy.
Zalecana:
Jak rozwiązać równanie kwadratowe za pomocą prawa czynnika zerowego?

Z tego możemy wywnioskować, że: Jeśli iloczyn dowolnych dwóch liczb wynosi zero, to jedna lub obie liczby są zerowe. Oznacza to, że jeśli ab = 0, to a = 0 lub b = 0 (co obejmuje możliwość, że a = b = 0). Nazywa się to prawem czynnika zerowego; i często go używamy do rozwiązywania równań kwadratowych
Jak algebraicznie rozwiązać równanie wartości bezwzględnej?

ROZWIĄZYWANIE RÓWNAŃ ZAWIERAJĄCYCH WARTOŚCI BEZWZGLĘDNE Krok 1: Wyodrębnij wyrażenie wartości bezwzględnej. Krok 2: Ustaw ilość w notacji wartości bezwzględnej równą + i - ilość po drugiej stronie równania. Krok 3: Znajdź niewiadomą w obu równaniach. Krok 4: Sprawdź swoją odpowiedź analitycznie lub graficznie
Jak rozwiązać równanie nierówności liniowej?

Istnieją trzy kroki: Zmień układ równania tak, aby „y” było po lewej, a wszystko inne po prawej. Narysuj linię 'y=' (ustaw ją jako linię ciągłą dla y≤ lub y≥ i linię przerywaną dla y). „mniej niż” (y< lub y≤)
Jak rozwiązać równanie, izolując zmienną?
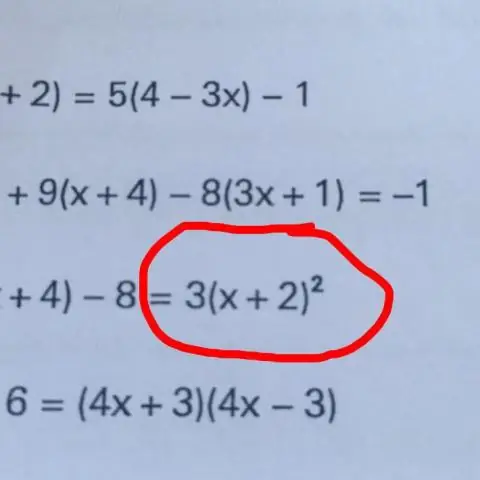
Podstawową techniką wyodrębniania zmiennej jest „zrobienie czegoś po obu stronach” równania, na przykład dodawanie, odejmowanie, mnożenie lub dzielenie obu stron równania przez tę samą liczbę. Powtarzając ten proces, możemy uzyskać zmienną izolowaną po jednej stronie równania
Jak rozwiązać równanie lub nierówność?

Aby rozwiązać nierówność, wykonaj następujące kroki: Krok 1 Wyeliminuj ułamki, mnożąc wszystkie wyrazy przez najmniejszy wspólny mianownik wszystkich ułamków. Krok 2 Uprość, łącząc podobne terminy po każdej stronie nierówności. Krok 3 Dodaj lub odejmij ilości, aby uzyskać nieznane z jednej strony i liczby z drugiej
