Spisu treści:
Wideo: Czy możemy wykonać regresję na danych nieliniowych?
2024 Autor: Miles Stephen | [email protected]. Ostatnio zmodyfikowany: 2023-12-15 23:39
Regresja nieliniowa może pasują do wielu innych rodzajów krzywych, ale to Móc wymagają więcej wysiłku zarówno w celu znalezienia najlepszego dopasowania, jak i interpretować rola zmiennych niezależnych. Dodatkowo R-kwadrat nie jest ważny dla regresja nieliniowa i nie da się Oblicz wartości p dla oszacowań parametrów.
Czy w ten sposób regresja może być nieliniowa?
W statystykach regresja nieliniowa jest formą regresja analiza, w której dane obserwacyjne są modelowane przez funkcję, która jest nieliniowy kombinacji parametrów modelu i zależy od jednej lub więcej zmiennych niezależnych. Dane są dopasowywane metodą kolejnych przybliżeń.
Można również zapytać, czy r kwadrat jest tylko dla regresji liniowej? Ogólne ramy matematyczne dla r - do kwadratu nie działa poprawnie, jeśli Model regresji nie jest liniowy . Pomimo tego, większość programów statystycznych nadal oblicza r - do kwadratu dla modeli nieliniowych. Jeśli użyjesz r - do kwadratu wybrać najlepsze Model prowadzi do właściwego tylko model 28-43% czasu.
W związku z tym, jak obliczyć regresję nieliniową?
Jeśli Twój model używa równanie w postaci Y = a0 + b1x1, to jest regresja liniowa Model. Jeśli nie, to nieliniowy.
Y = f(X, β) + ε
- X = wektor predyktorów p,
- β = wektor k parametrów,
- f(-) = znana funkcja regresji,
- ε = termin błędu.
Jakie są rodzaje regresji?
Rodzaje regresji
- Regresja liniowa. Jest to najprostsza forma regresji.
- Regresja wielomianowa. Jest to technika dopasowywania równania nieliniowego poprzez wielomianową funkcję zmiennej niezależnej.
- Regresja logistyczna.
- Regresja kwantylowa.
- Regresja grzbietowa.
- Regresja Lasso.
- Elastyczna regresja netto.
- Regresja głównych składowych (PCR)
Zalecana:
Jak wykonać regresję sinusoidalną na kalkulatorze?
WIDEO Jak obliczyć regresję sinusoidalną? Regresja sinusoidalna . Dostosuj wartości A, B, C i D w równanie y = A*sin(B(x-C))+D aby zrobić a sinusoidalny krzywa pasuje do danego zestawu losowo wygenerowanych danych. Gdy masz już dobrą funkcję, kliknij „Pokaż obliczone”, aby zobaczyć obliczone regresja linia.
Czy możemy uruchomić świetlówkę bez rozrusznika?
Uruchomienie zimnej rury bez rozrusznika wymaga innych środków generowania impulsu wysokiego napięcia, a ponieważ w zimnej rurze skondensowały się pary rtęci, wymaga to znacznie wyższego napięcia niż wcześniej. Ale gdy lampka się zaświeci, nagrzewa się wystarczająco, aby odparować resztę rtęci
Czy możemy stworzyć grawitację na Marsie?
Na przykład Mars ma masę 6,4171 x 1023 kg, co stanowi 0,107 masy Ziemi. Ma również średni promień 3389,5 km, co przekłada się na 0,532 promienia Ziemi. Grawitację powierzchniową Marsa można zatem wyrazić matematycznie jako: 0,107/0,532², z czego otrzymujemy wartość 0,376
Czy możemy zastosować trzecie prawo Newtona do siły grawitacji?
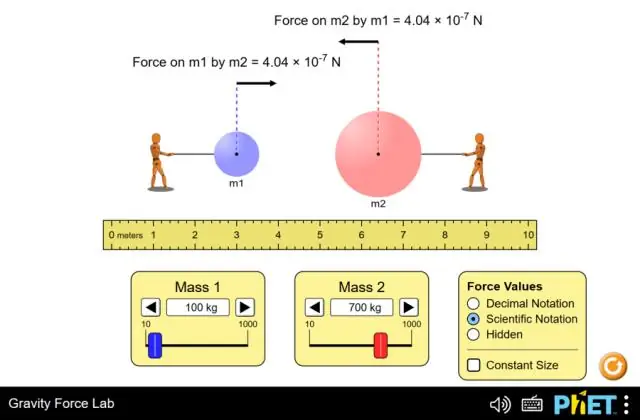
Tak, trzecie prawo Newtona ma zastosowanie do siły grawitacji. Oznacza to zatem, że kiedy nasza Ziemia wywiera siłę przyciągania na obiekt, to ten obiekt również wywiera taką samą siłę na Ziemię, w przeciwnym kierunku. Dlatego możemy powiedzieć, że możesz zastosować trzecie prawo Newtona do siły grawitacji
Która metoda klasyfikacji danych umieszcza taką samą liczbę rekordów lub jednostek analizy w każdej klasie danych?
Kwantyl. każda klasa zawiera równą liczbę cech. Klasyfikacja kwantylowa dobrze nadaje się do danych o rozkładzie liniowym. Kwantyl przypisuje tę samą liczbę wartości danych do każdej klasy