Wideo: Co to jest dwuwarunkowe stwierdzenie w przykładzie geometrii?
2024 Autor: Miles Stephen | [email protected]. Ostatnio zmodyfikowany: 2023-12-15 23:39
ten oświadczenie r s jest prawdziwe z definicji warunkowego. ten oświadczenie s r również jest prawdziwe. Dlatego zdanie „Trójkąt jest równoramienny wtedy i tylko wtedy, gdy ma dwie przystające (równe) boki” jest dwuwarunkowy . Podsumowanie: A dwuwarunkowe oświadczenie jest zdefiniowany jako prawdziwy, gdy obie części mają tę samą wartość prawdziwości.
Co więcej, jaki jest przykład dwuwarunkowego oświadczenia?
Przykłady instrukcji dwuwarunkowych ten oświadczenia dwuwarunkowe dla tych dwóch zbiorów byłoby: Wielokąt ma tylko cztery boki wtedy i tylko wtedy, gdy wielokąt jest czworokątem. Wielokąt jest czworokątem wtedy i tylko wtedy, gdy wielokąt ma tylko cztery boki.
Co więcej, czym jest dwuwarunkowość w geometrii? A dwuwarunkowy Instrukcja jest kombinacją instrukcji warunkowej i jej odwrotności zapisanej w formie wtedy i tylko wtedy. Dwa odcinki linii są przystające wtedy i tylko wtedy, gdy mają taką samą długość. A dwuwarunkowy jest prawdziwe wtedy i tylko wtedy, gdy oba warunki są prawdziwe.
W związku z tym, kiedy możesz napisać dwuwarunkowe oświadczenie?
' Oświadczenia dwuwarunkowe są prawdziwe sprawozdania które łączą hipotezę i wniosek z kluczowymi słowami „jeśli i tylko wtedy. ' Na przykład oświadczenie będzie przyjmij tę formę: (hipoteza) wtedy i tylko wtedy, gdy (wniosek). Moglibyśmy także pisać w ten sposób: (wniosek) wtedy i tylko wtedy, gdy (hipoteza).
Co oznacza IFF w dwuwarunkowym oświadczeniu?
W logice i matematyce logika dwuwarunkowy , czasami znany jako materiał dwuwarunkowy , jest spójnikiem logicznym używanym do łączenia dwóch sprawozdania i tworzyć oświadczenie " wtedy i tylko wtedy ", gdzie jest znany jako poprzednik i następnik. Jest to często skracane jako „ jeśli ".
Zalecana:
Czym jest dwuwarunkowe stwierdzenie w logice?
Kiedy połączymy w ten sposób dwie instrukcje warunkowe, otrzymamy dwuwarunkowe. Definicja: Zdanie dwuwarunkowe jest zdefiniowane jako prawdziwe, gdy obie części mają tę samą wartość prawdy. Dwuwarunkowe p q reprezentuje „p wtedy i tylko wtedy, gdy q”, gdzie p jest hipotezą, a q jest wnioskiem
Co to jest połączony wykres wyjaśnić na przykładzie?
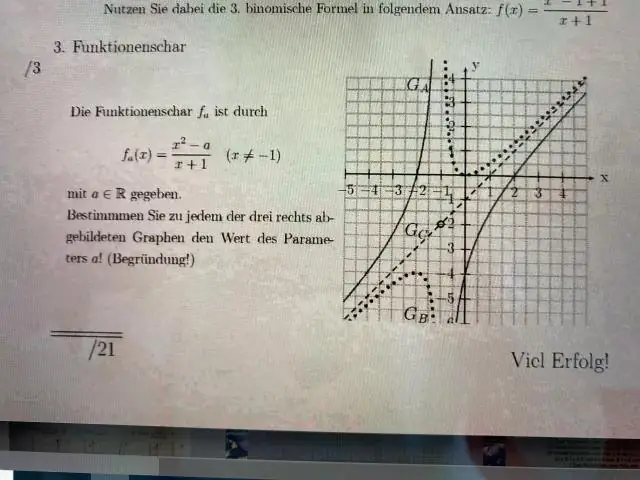
W całym wykresie istnieje krawędź pomiędzy każdą parą wierzchołków na wykresie. Drugi to przykład grafu połączonego. W grafie połączonym możliwe jest przejście z każdego wierzchołka grafu do każdego innego wierzchołka grafu poprzez szereg krawędzi, zwany ścieżką
Co to jest iloraz w przykładzie matematycznym?
Odpowiedź po podzieleniu jednej liczby przez drugą. dzielna ÷ dzielnik = iloraz. Przykład: w 12 ÷ 3 = 4, 4 jest ilorazem
Dlaczego słuszne jest stwierdzenie, że energia jest oszczędzana w maszynie?
Dlaczego można powiedzieć, że ENERGIA jest ZACHOWANA w maszynie? Energia jest zachowywana lokalnie (tj. może się poruszać, ale nie może skakać) wszędzie we wszechświecie. Twoja maszyna może „marnować” energię, zamieniając jej część w ciepło, ale w rzeczywistości nie możesz niszczyć ani wytwarzać energii
Czym jest izomeria geometryczna na przykładzie?
Izomery geometryczne to cząsteczki, które są zablokowane w swoich pozycjach przestrzennych względem siebie ze względu na podwójne wiązanie lub strukturę pierścieniową. Rozważmy na przykład następujące dwie cząsteczki