
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:39.
- Ostatnio zmodyfikowany 2025-06-01 05:05.
ten twierdzenie o resztach stwierdza, że f(a) jest reszta gdy wielomian f(x) dzieli się przez x - a. Tak więc, mając dany wielomian f(x), aby sprawdzić, czy dwumian liniowy postaci x - a jest czynnik wielomianu rozwiązujemy dla f(a). Jeśli f(a) = 0, to x - a jest a czynnik , a x - a nie jest a czynnik Inaczej.
Podobnie pyta się, jak działa twierdzenie o reszcie?
ten twierdzenie o resztach stwierdza co następuje: Jeśli podzielisz wielomian f(x) przez (x - h), wtedy reszta jest f(h). ten twierdzenie stwierdza, że nasz reszta równa się f(h). Dlatego my robić nie trzeba używać długiego dzielenia, ale wystarczy obliczyć wielomian, gdy x = h, aby znaleźć reszta.
Można też zapytać, co oznacza reszta z 0? Jeśli x - c jest współczynnikiem, możesz przepisać oryginalny wielomian jako (x - c) (iloraz). W rozwiązaniu tego typu problemu możesz wykorzystać podział syntetyczny. ten Reszta Twierdzenie mówi, że f(c) = the reszta . Więc jeśli reszta okazuje się być 0 kiedy zastosujesz dzielenie syntetyczne, to x - c jest współczynnikiem f(x).
Co więcej, jaki jest sens twierdzenia o reszcie?
ten Twierdzenie o reszcie mówi, że możemy przedefiniować wielomian jako dzielnik, a następnie obliczyć wielomian przy x = a. Ale kiedy x = a, czynnik „x - a” wynosi po prostu zero!
Czy zero jest resztą?
Kiedy jeden składnik („dywidenda”) jest podzielony przez inny składnik („dzielnik”), wynikiem jest „iloraz” i „ reszta . Kiedy reszta to zero , zarówno iloraz, jak i dzielnik są czynnikami dywidendy. 0 to reszta . Ponieważ reszta to zero , zarówno 2, jak i 3 są dzielnikami 6.
Zalecana:
Które twierdzenie najlepiej uzasadnia, dlaczego proste J i K muszą być równoległe?

Twierdzenie o przeciwnych naprzemiennych kątach zewnętrznych uzasadnia, dlaczego proste j i k muszą być równoległe. Twierdzenie o przeciwnych alternatywnych kątach zewnętrznych mówi, że jeśli dwie linie są przecięte przez poprzeczkę, tak że naprzemienne kąty zewnętrzne są przystające, to linie są równoległe
Co to jest twierdzenie o środkowej części trapezu?

Twierdzenie o trapezie środkowym. Twierdzenie o midsegmentu trójkąta mówi, że linia łącząca punkty środkowe dwóch boków trójkąta, zwana midsegmentem, jest równoległa do trzeciego boku, a jej długość jest równa połowie długości trzeciego boku
Dlaczego bufor działa najlepiej przy pH zbliżonym do jego pKa?
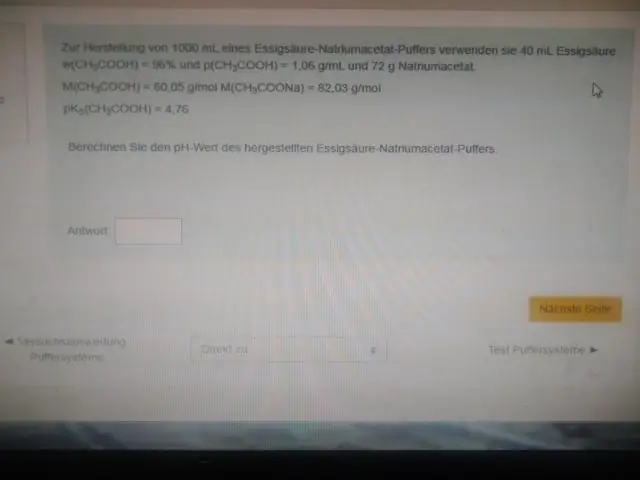
Innymi słowy, pH równomolowego roztworu kwasu (np. gdy stosunek stężenia kwasu i sprzężonej zasady wynosi 1:1) jest równe pKa. Region ten jest najbardziej skuteczny w przeciwdziałaniu dużym zmianom pH po dodaniu kwasu lub zasady. Krzywa miareczkowania wizualnie pokazuje pojemność buforową
Dlaczego działa zasada ciągłości bocznej?

Zasada ciągłości bocznej stwierdza, że warstwy osadów początkowo rozciągają się na boki we wszystkich kierunkach; innymi słowy, są bocznie ciągłe. W rezultacie można założyć, że skały, które pod innymi względami są podobne, ale są teraz oddzielone doliną lub inną cechą erozji, są pierwotnie ciągłe
Dlaczego zasada Archimedesa działa?

Jeśli siła wyporu jest większa niż ciężar obiektu, obiekt uniesie się na powierzchnię i unosi się. Zasada Archimedesa mówi, że siła wyporu działająca na obiekt jest równa ciężarowi wypieranego przez niego płynu. Ciężar właściwy to stosunek gęstości obiektu do płynu (zwykle wody)
