Wideo: Jak znaleźć prędkość z przyspieszeniem i czasem?
2024 Autor: Miles Stephen | [email protected]. Ostatnio zmodyfikowany: 2023-12-15 23:39
Jeśli przyśpieszenie jest stała, więc przyśpieszenie = zmiana w prędkość / czas za tę zmianę. Więc zmiana w prędkość jest przyśpieszenie razy czas . Nadal musisz znać inicjał prędkość które dodajesz do zmiany. (Gdyby przyśpieszenie nie jest stały, potrzebujesz rachunku różniczkowego.)
W ten sposób, jak znaleźć przyspieszenie z prędkością?
Obliczanie przyspieszenia obejmuje dzielenie prędkość przez czas - lub w jednostkach SI, dzieląc metr na sekundę [m/s] przez sekundę [s]. Dwukrotne dzielenie odległości przez czas jest tym samym, co dzielenie odległości przez kwadrat czasu przyśpieszenie to metr na sekundę do kwadratu.
Następnie pojawia się pytanie, jak oceniasz prędkość w zależności od odległości i czasu? Możesz użyć równoważnego wzoru d = rt, co oznacza dystans równa się stawce razy czas . Do rozwiązania dla prędkość lub oceń użyj wzoru na prędkość , s = d/t co oznacza prędkość równa się dystans podzielony przez czas . Do rozwiązania dla czas użyj wzoru na czas , t = d/s co oznacza czas równa się dystans podzielony przez prędkość.
Co więcej, jak znaleźć prędkość, mając dane przyspieszenie i czas?
Do obliczyć prędkość za pomocą przyśpieszenie , zacznij od pomnożenia przyśpieszenie przez zmianę w czas . Na przykład, jeśli przyśpieszenie wynosi 10 m/s2 a zmiana w czas wynosi 5 sekund, to jest wzrost 50 m/wzrost prędkość . Następnie dodaj inicjał prędkość do wzrostu w prędkość.
Jaka jest formuła przemieszczenia?
Wprowadzenie do Przemieszczenie i AccelerationEquation brzmi: Przemieszczenie równa się pierwotnej prędkości pomnożonej przez czas plus połowa przyspieszenia pomnożonego przez kwadrat czasu. Oto przykładowy problem i jego rozwiązanie pokazujące zastosowanie tego równania: Obiekt porusza się z prędkością 5,0 m/s.
Zalecana:
Jak znaleźć średnią prędkość przy dwóch prędkościach?
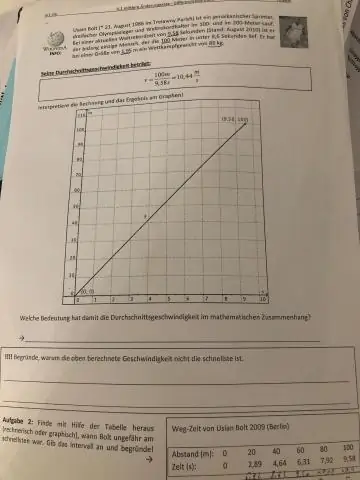
Suma prędkości początkowej i końcowej jest dzielona przez 2, aby znaleźć średnią. Kalkulator średniej prędkości wykorzystuje wzór, który pokazuje, że średnia prędkość (v) jest równa sumie prędkości końcowej (v) i prędkości początkowej (u), podzielonej przez 2
Jak znaleźć prędkość kątową i przyspieszenie?
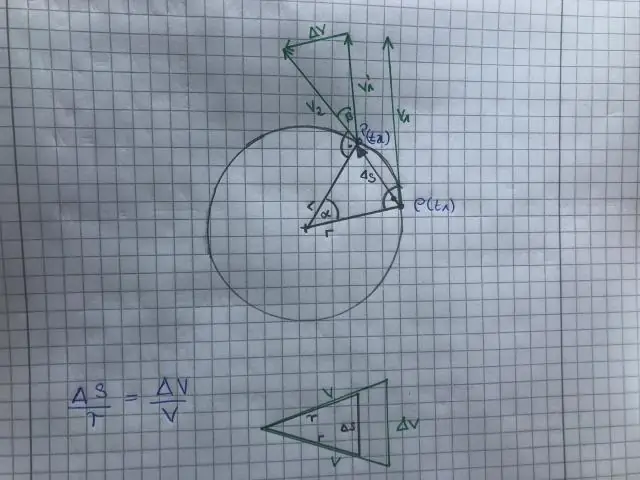
W postaci równania przyspieszenie kątowe wyraża się następująco: α=Δ&Δt α = Δ ω Δ t, gdzie Δω jest zmianą prędkości kątowej, a Δt jest zmianą w czasie. Jednostki przyspieszenia kątowego to (rad/s)/s lub rad/s2
Jak prędkość może się zmienić, gdy prędkość nie?
Prędkość jest wielkością wektorową, co oznacza, że wskazuje wielkość i kierunek. Tak więc jednym ze sposobów zmiany prędkości obiektu bez zmiany prędkości jest zmiana jego kierunku. Przykładem tego jest ruch okrężny, w którym obiekt zawsze zmienia kierunek, mając stałą prędkość
Jaka jest średnia prędkość i prędkość?
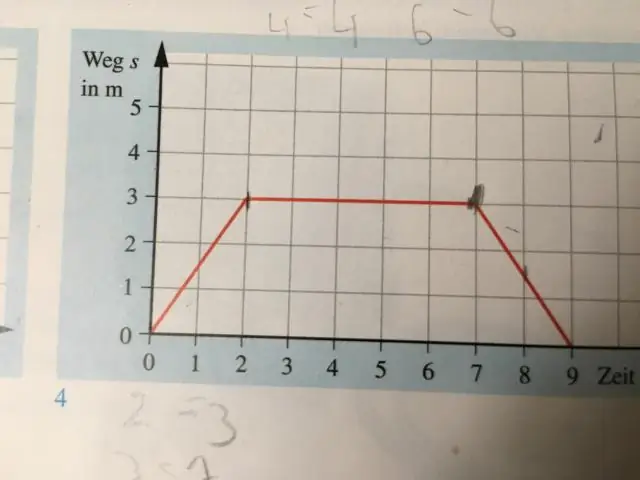
Średnia prędkość i średnia prędkość to dwie różne wielkości. W prostych słowach średnia prędkość to szybkość, z jaką porusza się obiekt i jest wyrażona jako całkowita odległość podzielona przez całkowity czas. Średnia prędkość może być zdefiniowana jako całkowite przemieszczenie podzielone przez całkowity czas
Co oznaczają prędkość i prędkość?
Podsumowując, prędkość i prędkość to wielkości kinematyczne, które mają wyraźnie różne definicje. Szybkość, będąca wielkością skalarną, to szybkość, z jaką obiekt pokonuje odległość. Średnia prędkość to odległość (wielkość skalarna) na stosunek czasu. Prędkość to tempo, w jakim zmienia się pozycja