- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:39.
- Ostatnio zmodyfikowany 2025-01-22 17:07.
Aby utworzyć powiększenie za pomocą Współczynnik skali z '' 2 '': Narysuj proste linie łączące każdy wierzchołek ze środkiem rozszerzanie się . Użyj kompasu, aby znaleźć punkty, które znajdują się w odległości dwukrotnie większej od środka rozszerzanie się jako oryginalne wierzchołki. Połącz nowe wierzchołki, aby utworzyć rozszerzone obraz.
Podobnie, pyta się, w jaki sposób rozszerzasz się o współczynnik skali 2?
Rozszerzanie się z współczynnik skali 2 , pomnożyć przez 2 . Zaczynając od czworoboku ABCD (niebieski), narysuj rozszerzanie się obraz czworoboku ze środkiem na początku i a Współczynnik skali ½. Każdy wierzchołek ABCD jest mnożony przez ½. Rozszerzanie się z Współczynnik skali ½, pomnóż przez ½.
Dodatkowo jaka jest zasada dylatacji? Notacja reguła ma następującą postać Dk(x, y)=(kx, ky) i mówi, że obraz wstępny przeszedł a. rozszerzanie się o pochodzeniu przez współczynnik skali k. Jeśli k jest większe niż jeden, rozszerzanie się obraz będzie większy niż. wstępny obraz. Jeśli k jest między 0 a 1, rozszerzanie się obraz będzie mniejszy niż obraz wstępny.
Podobnie, pyta się, co oznacza poszerzenie o współczynnik skali 2?
Przykład 1. Poniższy rysunek przedstawia: rozszerzanie się z współczynnik skali 2 . Ten znaczy że obraz A' jest dwa razy większy niż obraz wstępny A. Podobnie jak w przypadku innych przekształceń, do odróżnienia obrazu od obrazu wstępnego używa się notacji pierwszej. Obraz zawsze ma pierwszą liczbę po literze, taką jak A'.
Jaki jest współczynnik skali 1 2?
Jako przykład pomyśl o dwóch podobnych kwadratach. Jeden ma długość boku 2 cale, a drugi ma długość boku 4 cale. Daje to współczynnik skali 1: 2 od małego kwadratu do dużego kwadratu. Te dwa podobne kwadraty mają współczynnik skali 1: 2 od małego kwadratu do dużego kwadratu.
Zalecana:
Czy dylatacje zawsze zwiększają długość odcinków linii?

Podczas gdy skalują odległości między punktami, dylatacje nie zmieniają kątów. Transformacje wpływają na wszystkie punkty na płaszczyźnie, a nie tylko na poszczególne figury, które wybieramy do analizy podczas pracy z transformacjami. Wszystkie długości odcinków linii w płaszczyźnie są skalowane tym samym współczynnikiem, gdy stosujemy dylatację
Jak skonstruować prostopadły odcinek linii?
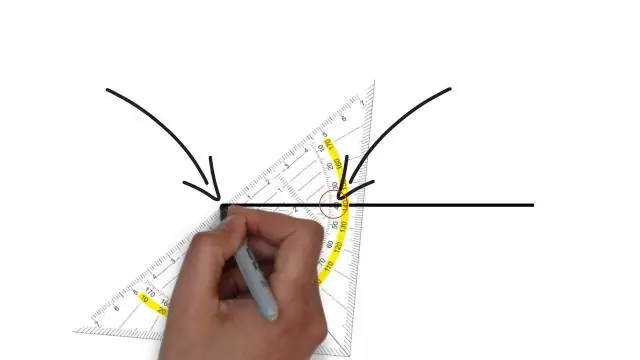
Konstrukcja: linia przechodząca przez P prostopadle do danej linii. KROKI: Umieść punkt kompasu na P i przesuń łuk o dowolnej wielkości, który dwukrotnie przecina linię. Umieść punkt kompasu w jednym z dwóch miejsc, w których łuk przecina linię i wykonaj mały łuk poniżej linii (po stronie, gdzie nie znajduje się P)
Jak skonstruować kopię kątownika za pomocą kompasu?
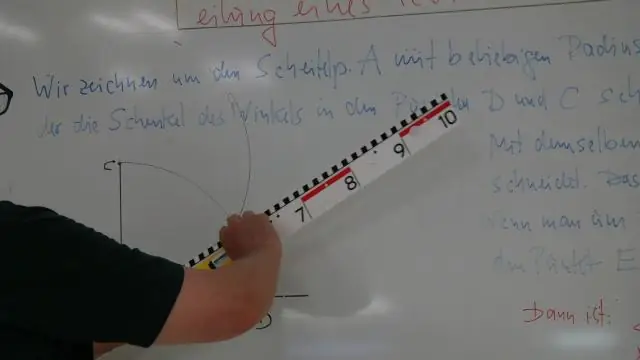
Jak skopiować kąt za pomocą kompasu Narysuj linię roboczą l z punktem B na niej. Otwórz kompas na dowolny promień r i utwórz łuk (A, r) przecinający dwa boki kąta A w punktach Piasek T. Skonstruuj łuk (B, r) przecinający linię lw pewnym punkcieV. Skonstruuj łuk (S, ST). Skonstruuj łuk (V, ST) łuk przecinający się (B, r) w punkcieW
Jak skonstruować prostopadły?
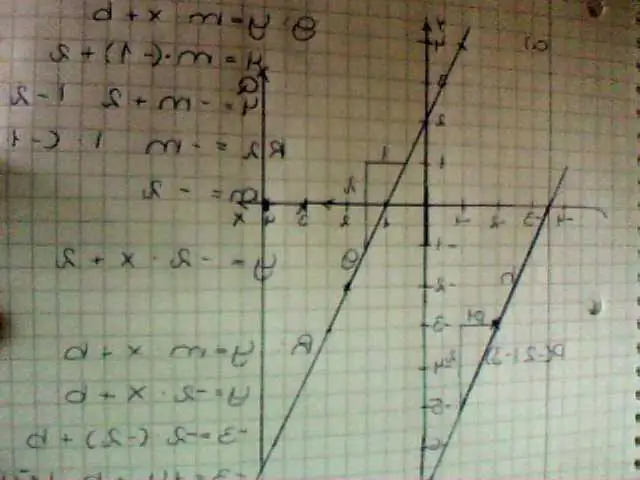
Konstrukcja: linia przechodząca przez P prostopadle do danej linii. KROKI: Umieść punkt kompasu na P i przesuń łuk o dowolnej wielkości, który dwukrotnie przecina linię. Umieść punkt kompasu w jednym z dwóch miejsc, w których łuk przecina linię i wykonaj mały łuk poniżej linii (po stronie, gdzie nie znajduje się P)
Jak skonstruować płaszczyznę współrzędnych w geometrii?
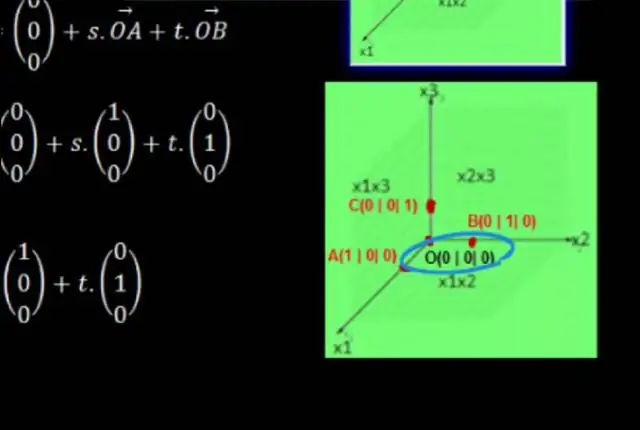
Aby utworzyć płaszczyznę współrzędnych, wykonaj następujące kroki: Narysuj dwie linie liczbowe prostopadłe do siebie, przecinające się w punkcie 0 na obu liniach. Oznacz poziomą linię liczbową jako oś x i oznacz pionową linię liczbową jako oś y
