Wideo: Jak znaleźć drugą pochodną funkcji trygonometrycznej?
2024 Autor: Miles Stephen | [email protected]. Ostatnio zmodyfikowany: 2023-12-15 23:39
WIDEO
A więc, jakie są pochodne 6 funkcji trygonometrycznych?
Pochodne funkcji trygonometrycznych. Podstawowe funkcje trygonometryczne obejmują 6 funkcji: sinus ( grzech x), cosinus ( sałata x), tangens (tanx), cotangens (cotx), sieczną (secx) i cosecans (cscx). Wszystkie te funkcje są ciągłe i różniczkowalne w swoich dziedzinach.
Następnie pojawia się pytanie, jaka jest pochodna 1? ten Pochodna mówi nam nachylenie funkcji w dowolnym punkcie. Istnieją zasady, których możemy przestrzegać, aby znaleźć wiele pochodne . Na przykład: nachylenie o stałej wartości (np. 3) wynosi zawsze 0.
Pochodna Zasady.
| Wspólne funkcje | Funkcjonować | Pochodna |
|---|---|---|
| Stały | C | 0 |
| Linia | x | 1 |
| topór | a | |
| Kwadrat | x2 | 2x |
Ludzie pytają też, jaka jest 27. pochodna COSX?
grzech
Co to jest cos 2x?
sałata ( 2x ) = sałata (x + x) = sałata (x) sałata (x) - sin(x)sin(x) = sałata ^ 2(x ) - grzech^ 2(x ) Biorąc pod uwagę pitagorejskie tożsamości: (sin^ 2(x ) + sałata ^ 2(x ) = 1), sałata ^ 2(x ) = 1 - grzech^ 2(x ) więc sałata ( 2x ) również równa się (1 - grzech^ 2(x )) - grzech^ 2(x ) lub 1 - 2sin^ 2(x )
Zalecana:
Jak znaleźć symboliczną reprezentację funkcji kwadratowej?
Funkcje kwadratowe można przedstawić symbolicznie za pomocą równania, y(x) = ax2 + bx + c, gdzie a, b i c są stałymi, a a ≠ 0. Formularz ten nazywany jest formularzem standardowym
Jak znaleźć częstotliwość progową funkcji pracy?
Aby to obliczyć, będziesz potrzebować energii światła padającego na materiał oraz energii kinetycznej wyrzuconego fotoelektronu. Używając E = hf możemy obliczyć częstotliwość światła, dodając energię i wyliczając f. To będzie częstotliwość progowa
Jak znaleźć w funkcji kwadratowej?
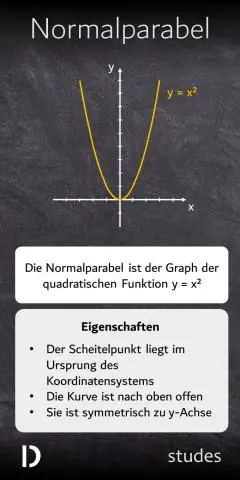
Mówi się, że funkcja kwadratowa f(x) = a(x-h)2 + k, a nie równa się zeru, ma postać standardową. Jeśli a jest dodatnie, wykres otwiera się w górę, a jeśli jest ujemne, to otwiera się w dół. Linia symetrii to linia pionowa x = h, a wierzchołek to punkt (h,k)
Jak znaleźć maksymalną wartość funkcji kwadratowej?
Jeśli otrzymasz formułę y = ax2 + bx + c, możesz znaleźć maksymalną wartość za pomocą wzoru max = c- (b2 / 4a). Jeśli masz równanie y = a(x-h)2 + k, a teatr jest ujemny, to maksymalna wartość wynosi k
Jak znaleźć dziedzinę funkcji algebraicznej?
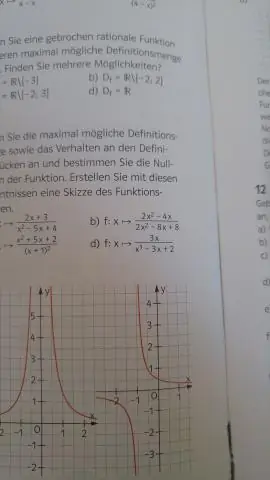
Dziedziną funkcji jest zbiór wszystkich możliwych danych wejściowych dla funkcji. Na przykład dziedzina f(x)=x² to wszystkie liczby rzeczywiste, a dziedzina g(x)=1/x to wszystkie liczby rzeczywiste z wyjątkiem x=0